การแก้ระบบสมการเชิงเส้นที่จำนวนตัวแปร 2 หรือ 3 ตัว เราอาจจะสามารถใช้วิธีย้ายสมการและการแทนค่าในสมการ เพื่อหาคำตอบได้ โดยไม่ยุ่งยากนัก แต่หากจำนวนตัวแปรมีหลายตัวมากขึ้นการใช้วิธแทนค่าสมการจะยุ่งยากมาก เราจึงใช้ระบบ Matrix ในการแก้ปัญหา ซึ่งการแก้ปัญหาโดยระบบ Matrix ก็มีหลายวิธีการ หนึ่งในนั้นคือวิธี Gaussian elimination ซึ่งเป็นวิธีที่เรียบง่าย จะว่าไปก็คล้ายกับการแทนค่าสมการ แต่เราจะทำเป็นระบบ
หลักการของวิธี Gaussian elimination คือ ทำให้ Matrix กลายเป็น Upper triangular matrix โดยใช้วิธีการดำเนินการที่ละคู่ของแถว ลองดูตามตัวอย่าง สมการ 3 ตัวแปร ต่อไปนี้
เขียนในรูป Matrix
สร้าง Augmented Matrix เพื่อเตรียมดำเนินการ โดยนำ vector ค่าคงที่ มาใส่เป็น column สุดท้ายของ matrix สัมประสิทธิ์
ผลลัพธ์ของ augmented matrix เมื่อผ่านขั้นที่ 1
ขั้นที่ 2 ทำค่าแรกของ row ที่ 3 ให้เป็นศูนย์ โดยนำ factor (3/2)*(-1) คูณกับทั้งแถวของแถวที่ 3 แล้ว นำไปบวกกับแถวที่ 1
ผลลัพธ์ของ augmented matrix เมื่อผ่านขั้นที่ 2
ขั้นที่ 3 ทำค่าที่ 2 ของ row ที่ 3 ให้เป็นศูนย์ โดยนำ factor (4/-3.5)*(-1) คูณกับทั้งแถวของแถวที่ 3 แล้ว นำไปบวกกับแถวที่ 2
แตก augmented matrix กลับไปอยู่ในรูปสมการ จะเห็นว่า matrix สัมประสิทธิ์ กลายเป็น upper triangular matrix เรียบร้อยแล้ว
ขั้นตอนต่อไปเรียกว่าการแทนค่าย้อนกลับ (Backward substitution) โดยไล่มากจากแถวล่างสุดซึ่งเหลือตัวแปรเดียว
หาตัวแปร y จากแถวที่ 2
หาตัวแปร x จากแถวที่ 1
เป็นอันว่าเสร็จสิ้นการแก้ระบบสมการเชิงเส้น
บางตำรานิยามกระบวนการของวิธี Gaussian Elimination ไว้แค่เสร็จสิ้นขั้นตอนทำ upper triangular matrix แต่เมื่อรวมกระบวนการ Backward substitution เข้าไปด้วยจะเรียกว่า Gauss-Jordan Elimination
ลองตรวจคำตอบ โดยให้โปรแกรม MathCAD ช่วยหาคำตอบ โดยใช้ inverse ของ matrix สัมประสิทธิ์ คุณกับ vector ของค่าคงที่

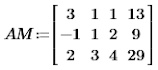










ไม่มีความคิดเห็น:
แสดงความคิดเห็น