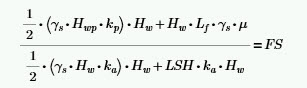Mechanics of Reinforced Concrete Beam Section - กลไกของหน้าตัดคานคอนกรีตเสริมเหล็ก (EP-3) - คำนวณกำลังหน้าตัด ULS

 บทนำ

     ในบทความนี้เราจะมาคำนวณกำลังของหน้าตัดที่จุดวิบัติ ซึ่งหน้าตัดที่จุดวิบัติแบ่งได้เป็น 3 สถานะ ตามค่า strain ของเหล็กเสริม

     เป็นหน้าตัดแบบ tension controlled section - เมื่อ tensile strain มีค่ามากกว่า 0.005 ขึ้นไป

     เป็นหน้าตัดแบบ transition - เมื่อ tensile strain ในเหล็กเสริมมีค่า ระหว่าง 0.002 - 0.005

     เป็นหน้าตัดแบบ compression controlled section - เมื่อ tensile strain ในเหล็กเสริมมีค่า น้อยกว่า 0.002 ลงมา

     * เมื่อ tensile strain ในเหล็กเสริมมีค่า 0.003 เท่ากับ compressive strain ของคอนกรีต เรียกสถานะนี้ว่า Balanced strain condition 

    โดยปกติแล้วเราจะออกแบบหน้าตัดคานให้อยู่ในช่วง tension controlled section  พฤติกรรมการวิบัติของหน้าตัดในช่วงนี้จะมีความเหนียว (Ductile Failure)  ก่อนวิบัติจะเกิด deflection มาก ช่วยเป็นสัญญานเตือนอันตรายได้  หรือหากเป็นคานต่อเนื่องก็จะช่วย redistribute โมเมนต์ไปจุดอื่นได้ หน้าตัดแบบนี้เมื่อถึงจุดวิบัติแล้วจะยังคงรับแรงได้อยู่

     

     ในทางตรงกันข้าม หากหน้าตัดอยู่ในช่วง compression controlled section พฤติกรรมการวิบัตินะเป็นแบบเปราะ (Brittle Failure)  ซึ่งเป็นการวิบัติแบบทันทีทันใด ไม่มีสัญญาณเตือนใดๆ   กำหลังหน้าตัดสูญสลายไปทันทีเมื่อคอนกรีตระเบิดออก  ( ถ้าจำเป็นต้องใช้งานหน้าตัดแบบนี้เราจะเพิ่มอัตราส่วนความปลอดภัยให้มากขึ้น โดยใช้ตัวคูณลดกำลังที่ 0.65 )

     มีสองวิธีการที่เราจะใช้คำนวณกำลัง

     1. คำนวณแบบง่าย - คำนวณกำลังหน้าตัดโดยตั้งสมมติฐานไว้ก่อนว่า เหล็กถึงจุด yield  จากนั้นคำนวณหา neutral axis แล้วจึงไปเช็ค tensile strain อีกที  หากพบว่า ถึงจุด yield  แสดงว่าตำแหน่ง neutral axis ที่คำนวณได้เป็นตำแหน่งที่ถูกต้อง กำลังของหน้าตัดก็จะเป็นค่าที่ถูกต้อง  แต่หากพบว่า tensile strain ไม่ถึงจุด yield แสดงว่าตำแหน่ง neutral axis ไม่ใช่ค่าที่ถูกต้อง กำลังของหน้าตัดที่คำนวณได้จะเป็นค่าประมาณเท่านั้น  ( ในทางปฏิบัตสำหรับคานคอนกรีตเสริมเหล็ก หากคำนวณแล้วพบว่าเหล็กไม่ yield นั่นแสดงว่าคานมีหน้าตัดลึกน้อยเกินไปเมื่อเทียบกับปริมาณเหล็กที่ใส่ ควรเพิ่มความลึกหน้าตัด )

     2. คำนวณโดยการ Trial  - หาตำแหน่ง neutral axis ที่ทำให้แรงในหน้าตัดสมดุลย์   โดยสมมติตำแหน่ง neutral axis มาค่าหนึ่ง จากนั้นคำนวณ strain ในเหล็กเสริม คำนวณแรงดึงทีสอดคล้องกับ strain ที่คำนวณได้  จากนั้นเช็ค balance ของแรงอัดกับแรงดึง ถ้ายังไม่ balance ก็กลับไปสมมติตำแหน่ง neutral axis ใหม่ ทำวนไปจนกว่าแรงอัดกับแรงดึงจะสมดุลย์   เมื่อแรงภายในสมดุลย์แล้วก็ไปคำนวณกำลังของหน้าตัด

วิธีการคำนวณแบบง่าย

     ในการคำนวณเราจะสมมติให้คอนกรีตถึงจุดวิบัติ โดยใช้ค่า strain ที่ผิวคอนกรีตเท่ากับ 0.003   และสมมติการกระจายของหน่วยแรงเป็นทรงสี่เหลี่ยม (rectangular stress block)  FBD ของสมมติฐานตั้งต้นเป็นดังภาพต่อไปนี้

ลองคำนวณกำลังหน้าตัดแบบที่เหล็กเสริม yield

ลองคำนวณกำลังหน้าตัดแบบที่เหล็กเสริมไม่ yield

วิธีการคำนวณแบบ strain compatibility

เริ่มด้วยการเขียนสมการเพื่อจำลองพฤติกรรมการ yield ของเหล็กเสริม

วิธีการคำนวณคือ เราจะ trial ค่า cNA ไปเรื่อยๆ จนกว่าแรงในหน้าตัดจะสมดุลย์ คือ eq.5 มีค่าเข้าใกล้ศูนย์  โดยเราคำนวณค่าแรงในเหล็กเสริมตาม strain ที่เกิดขึ้นจริง

ต่อไปลองใช้วิธีนี้คำนวณค่ากำลังของหน้าตัด จากตัวอย่างที่ผ่านมา ซึ่งเป็นแบบเหล็กไม่ yield เราลองมาดูว่าค่าที่ถูกต้องจะเป็นเท่าไร

สรุป

     วิธีอย่างง่ายสามารถใช้คำนวณกำลังของหน้าตัดได้ แต่คำตอบที่ได้จะถูกต้องเมื่อเหล็ก yield เท่านั้น หากเหล็กไม่ yield จะได้แค่คำตอบโดยประมาณ  แต่ทั้งนี้หน้าตัดโดยส่วนใหญ่ก็จะออกแบบให้เหล็ก yield อยู่แล้ว  หากพบว่าเหล็กไม่ yield ก็เปลี่ยนหน้าตัด

     วิธี strain compatibility จะได้ค่าที่ถูกต้องเสมอ เพราะคำนวณแรงในเหล็กตาม strain ที่เกิดขึ้นจริง 

    

Mechanics of Reinforced Concrete Beam Section - กลไกของหน้าตัดคานคอนกรีตเสริมเหล็ก (EP-2) - คำนวณกำลังหน้าตัด SLS

บทนำ 

     บทความนี้เรามาลองคำนวณกำลังของหน้าตัดคอนกรีตเสริมเหล็ก โดยจะลองคำนวณเปรียบเทียบกันใน 3 สถานะ คือ

     1. หน้าตัดคอนกรีตล้วน

     2. หน้าตัดคอนกรีตเสริมเหล็ก แบบไม่แตกร้าว

     3. หน้าตัดคอนกรีตเสริมเหล็ก แบบแตกร้าว 

หน้าตัดคอนกรีตล้วน

     สมมติคุณสมบัติ คอนกรีต ดังต่อไปนี้

     

     

     จากการคำนวณจะเห็นว่า หน้าตัดวิบัติโดยแรงดึง รับกำลังได้เพียง 1 ใน 4 เมื่อเทียบกับกำลังที่คอนโทรลโดยแรงอัด ซึ่งเป็นค่าที่หน้าตัดสามารถไปถึงได้หากไม่วิบัติโดยเเรงดึงเสียก่อน ดังนั้นในการคำนวณต่อไปเราจะนำเหล็กเข้ามาช่วยรับแรงดึงในหน้าตัด แล้วดูว่าจะเพิ่มกำลังของหน้าตัดได้อย่างไร

หน้าตัดคอนกรีตเสริมเหล็ก ( ไม่แตกร้าว )

สมมติคุณสมบัติเหล็กเสริม

พิจารณา FBD ของหน้าตัด ไม่แตกร้าว

จะเห็นว่าการเสริมเหล็กเข้าไป ช่วยเพิ่ม moment of inertia ของหน้าตัดช่วงไม่แตกร้าว  ซึ่งในที่นี้มีค่าเพิ่มขึ้น 12%

ต่อไปลองคำนวณกำลังของหน้าตัด

จะเห็นว่าเหล็กเสริมช่วยให้หน้าตัดก่อน crack มีกำลังเพิ่มขึ้น 17.5% จากหน้าตัดคอนกรีตล้วนที่วิบัติด้วยแรงดึง   แต่ยังมีค่าเพียง 30% ของกำลังที่ควรจะทำได้ของหน้าตัด

ต่อไปลองคำนวณโดยเพิ่มปริมาณเหล็กเสริมหลายๆค่า แล้วลองดูแนวโน้มของการเปลี่ยนแปลง ในการคำนวณได้คำนึงถึงการเรียงเหล็กเสริมเป็นชั้นๆด้วย ดังนั้นที่ปริมาณเหล็กเพิ่มขึ้น ค่า d จะลดลง

โดยจากผลการคำนวณสามารถแสดงเป็นกราฟความสัมพันธ์ระหว่าง การเพิ่มขึ้นของ moment of inertia กับปริมาณเหล็กเสริมได้ดังต่อไปนี้

จากกราฟด้านบน เส้นต่างๆเป็นตัวแทนของการใช้ขนาดเหล็กเสริมแต่ละขนาด จะเห็นว่าเหล็กเสริมขนาดใหญ่ มีประสิทธิภาพในการเพิ่มคุณสมบัติของหน้าตัดมากกว่า เหล็กเสริมขนาดเล็ก  โดยสำหรับหน้าตัดที่ทำการคำนวณ ได้ค่าสูงสุดของการเพิ่มขึ้นของค่า moment of inertia อยู่ที่ 31.5 %  ในช่วงหน้าตัดไม่แตกร้าว

ต่อไปลองดูผลการคำนวณในทำนองเดียวกัน ในรูปของ กำลังที่เพิ่มขึ้น กับ ปริมาณเหล็กเสริม แสดงดังต่อไปนี้

จะเห็นผลคล้ายกัน คือเหล็กขนาดใหญ่ มีประสิทธิภาพดีกว่าเหล็กขนาดเล็ก  โดยมีอัตราเพิ่มกำลังสูงสุดที่ 54.6 % ในช่วงหน้าตัดไม่แตกร้าว

หน้าตัดคอนกรีตเสริมเหล็ก ( แตกร้าว )

ต่อไปลอดูพฤติกรรมหลังการแตกร้าวของหน้าตัด พิจารณา FBD ของหน้าตัดแตกร้าวดังต่อไปนี้

จากผลการคำนวณแสดงให้เห็นว่า หลังการแตกร้าว moment of inertia ของหน้าตัดลดลง เหลือประมาณ 45% ของหน้าตัดคอนกรีตล้วน

ต่อไปลองคำนวณกำลังของหน้าตัดแตกร้าว  โดยกำหนดหน่วยแรงอัด 40% ของกำลังประลัย

จะเห็นว่ากำลังของหน้าตัดแตกร้าว เพิ่มขึ้น 183% จากหน้าตัดคอนกรีตล้วนซึ่งวิบัติด้วยแรงดึง  และมีค่า 72.4% ของกำลังที่ควรจะทำได้ของหน้าตัด

ต่อไปเราลองคำนวณโดยเปลี่ยนปริมาณเหล็กเสริมหลายๆค่า

โดยจากผลการคำนวณสามารถแสดงเป็นกราฟความสัมพันธ์ระหว่าง การเพิ่มขึ้นของ moment of inertia กับปริมาณเหล็กเสริมได้ดังต่อไปนี้

จากกราฟจะเห็นว่าที่ปริมาณเหล็กเสริม 3.5 % จะทำให้ได้ค่า moment of inertia 93.7% เมื่อเทียบกับหน้าตัดคอนกรีตล้วน นั่นเป็นค่าทางทฤษฎี  แต่ในความเป็นจริงเราจะเสริมเหล็กอยู่ในปริมาณ 1.0-1.5% ของหน้าตัดเท่านั้น  ซึ่งที่ปริมาณเหล็ก 1.5% ของหน้าตัดมีค่า moment of inertia อยู่ที่ 65% ของหน้าตัดคอนกรีตล้วนเท่านั้น

ต่อไปลองดูผลการคำนวณในทำนองเดียวกัน ในรูปของ กำลังที่เพิ่มขึ้น กับ ปริมาณเหล็กเสริม แสดงดังต่อไปนี้

จากกราฟจะเห็นว่าในทางทฏษฎีเราสามารถเพิ่มค่ากำลังได้มากถึง 290% เมื่อเทียบกับกำลังหน้าตัดคอนกรีตล้วนที่วิบัติโดยแรงดึง  แต่ในย่านการใช้งานที่ปริมาณเหล็ก 1.5 % จะเพิ่มกำลังได้ 244% เมื่อเทียบกับกำลังหน้าตัดคอนกรีตล้วนที่วิบัติโดยแรงดึง

คราวนี้เราจะลองเปรียบเทียบกับกำลังที่หน้าตัดควรจะรับได้ด้วย โดยแสดงผลดังต่อไปนี้

จะเห็นว่าที่ย่านการใช้งานที่ปริมาณเหล็ก 1.5% หน้าตัดจะมีกำลัง 87.6% ของที่ควรจะทำได้

สรุป

     จากที่คำนวณมาทั้งหมดเราจะเห็นว่า เป็นไปได้ในทางทฤษฎีที่จะใส่เหล็กมากจนหน้าตัดรับกำลังได้เต็มประสิทธิภาพ   แต่ในทางปฏิบัตินั้นเราไม่สามารถใส่เหล็กได้มากขนาดนั้นเพราะต้องคำนึงถึงการทำงานด้วย ปริมาณเหล็กที่แน่นเกินไปจะทำให้เทคอนกรีตได้ยากก่อให้เกิดปัญหาตามมาอีกมาก  ปัญหาสำคัญอีกประการคือ ราคา การยัดเหล็กเข้าไปมากๆ จะทำให้ราคาพุ่งสูงขึ้นเป็นเงาตามตัว

     จากการคำนวณเราจะเห็นประสิทธิภาพที่ขาดหาย  ซึ่งแน่นอนว่าวิศกรในอดีตก็เห็นเช่นกัน ในปี ค.ศ.1888  P.H.Jackson  เสนอแนวคิดที่สมบูรณ์แบบเกี่ยวกับการใช้งาน prestress concrete แต่ยังติดปัญหาเรื่องเทคโนโลยีของลวดอัดแรง ในขณะนั้นเทคโนโลยีลวดอัดแรงยังไม่ก้าวหน้ามากพอ จนในปี ค.ศ.1929  Eugène Freyssinet (1879-1962) ได้คิดค้นเทคโนโลยีคอนกรีตอัดแรง ประสิทธิภาพที่เคยขาดหายได้ถูกเติมเต็ม ทำให้โครงสร้างคอนกรีตเสริมเหล็กไปได้ไกลขึ้น โดยการใช้ลวดเหล็กกำลังสูงเข้ามาเป็นตัวหลักแทนที่เหล็กเสริมธรรมดา  ปัจจุบันคอนกรีตอัดแรงถูกใช้งานอย่างกว้างขวางทั้งงานสะพานและอาคาร

link สำหรับ file mathcad>>>https://drive.google.com/file/d/1AMFH3yFkCJtm-LRT-avawadxm9yS66rU/view?usp=sharing

Mechanics of Reinforced Concrete ฺBeam Section - กลไกของหน้าตัดคานคอนกรีตเสริมเหล็ก (EP-1)

บทนำ    

     บทความนี้นำเสนอกลไกการทำงานของหน้าตัดคอนกรีตเสริมเหล็ก  ซึ่งเป็นการนำวัสดุสองประเภทมาใช้งานร่วมกันเพื่อให้คุณสมบัติโดยรวมดีขึ้น  ในกรณีนี้เรามีคอนกรีตและเหล็ก คอนกรีตรับแรงอัดได้ดีมีราคาถูก แต่มีข้อด้อยกคือรับแรงดึงได้ต่ำมาก ส่วนเหล็กรับแรงได้ดีทังแรงอัดและแรงดึงมีกำลังสูงกว่าคอนกรีตมาก แต่ราคาก็แพงกว่าคอนกรีตมาก

     ถ้ามองในมุมของกำลังของหน้าตัดแล้ว แนวคิดในการใช้งานคอนกรีตเสริมเหล็กคือ ใช้เหล็กเข้ามาช่วยรับแรงดึงในหน้าตัด จะช่วยให้หน้าตัดรับแรงได้มากขึ้น

     หรือถ้ามองในมุมของราคา เรานำคอนกรีตเข้ามาแทนที่ส่วนที่รับแรงอัดในหน้าตัด คิดง่า่ยๆว่าเรามีหน้าตัดเหล็กล้วน เอาครึ่งหนึ่งออกไปแล้วแทนที่ด้วยคอนกรีตซึ่งมีราคาถูกกว่าเหล็กอย่างน้อย 10 เท่า ก็จะทำให้หน้าตัดของเรามีราคาถูกลงมาก

พฤติกรรมของหน้าตัดคอมโพสิท

     เราใช้หลักการ strain compatibility ในการคำนวณหน้าตัด composite  กล่าวคือ คำนวณ strain ก่อน จากนั้นใช้ความสัมพันธ์ stress-strain curve ของวัสดุ ในการคำนวณแรงในเนื้อวัสดุ

     ในกรณีหน้าตัดรับแรงดัด โดยทั่วไปสำหรับคานที่มีลักษณะเป็น "thin beam" เราใช้หลักการของ "Bernoulli-Euler beam theory" ซึ่งมีสมมติฐานหลัก 2 ประการคือ 

         1. plane sections remain plane - หมายถึง การเปลี่ยนแปลง strain ในหน้าตัดจะกระจายเป็นเส้นตรง

         2. small displacement - หลังรับแรงคานมีการเสียรูปน้อย

       * thin beam ในทางทฤษฎีหมายถึงคานที่มีอัตราส่วนความยาวต่อความลึกมากกว่า 20 เท่าขึ้นไป ที่อัตราส่วนนี้ผลของ shear deformation ในหน้าตัดจะมีค่าน้อยจนตัดทิ้งได้ ทำให้สามารถใช้ "Bernoulli-Euler beam theory" ได้  

         ** นอกจาก Bernoulli-Euler beam theory ซึ่งใช้กับ thin beam แล้ว เรายังมี Timoshenko-Ehrenfest beam theory ซึ่งใช้สำหรับ thick beam อีกด้วย

พฤติกรรมของวัสดุ

     พิจารณาจาก stress-strain curve จะเห็นว่าในช่วงใช้งาน เหล็กมีพฤติกรรมแบบ linear 

stress - strain curve of steel

ส่วนคอนกรีตเป็นแบบ non-linear ซึ่งพฤติกรรมของคอนกรีตนี้เองที่ทำให้การคำนวณมีความยุ่งยาก 

stress - strain curve of concrete

ช่วงพฤติกรรมของหน้าตัด

พิจารณาจากกราฟ stress-strain curve ของคอนกรีต  

     ที่จุดที่ 1 ที่ stress = 0.4 fcm เป็นจุดสิ้นสุดของพฤติกรรม Linear ของคอนกรีต ช่วงพฤติกรรมนี้ใช้คำนวณออกแบบระดับ SLS (Service Limit State) การกระจายของหน่วยแรงเป็นแบบ Linear ตามภาพต่อไปนี้

     ช่วงหลังจุดที่ 1 ไป  คอนกรีตมีพฤติกรรมแบบ Non-Linear  ซึ่งการคำนวณกำลังหน้าตัดช่วงนี้ทำได้ยุ่งยาก  เป็นโชคดีที่การออกแบบปกติเราไม่สนใจช่วงที่ยุ่งยากนี้

     ที่จุดที่ 2 เป็นจุดที่เราคำนวณกำลังของหน้าตัดที่ระดับ ULS (Ultimate Limit State) ซึ่งเราก็ใช้การ simplify การกระจายหน่วยแรงอัด จากที่เป็นการกระจายแบบ Non-Linear เป็นการกระจายแบบเส้นตรงคงที่ ทำให้การคำนวณง่ายขึ้น ตามภาพต่อไปนี้

สรุป

   ในตอนนี้เราได้ทราบหลักการเบื้องต้นของคอนกรีตเสริมเหล็กแล้ว  ในตอนต่อไปเราจะไปลองคำนวณกำลังของหน้าตัด..............

การคำนวณ - Deflection curve from BMD

     บทความนี้นำเสนอวิธีการหาการเสียรูปของคาน(Deflection) โดยคำนวณจากโมเมนต์ไดอะแกรม(BMD) 

    โดยสุดท้ายจะมีการคำนวณเปรียบเทียบระหว่างค่าที่ได้จากวิธีการที่นำเสนอ กับค่าที่ได้จากสูตรสำเร็จตามภาพด้านล่างนี้

หลักการ

     1. นำกราฟ BMD หารด้วย EI จะได้ Curvature ที่ตำแหน่งต่างๆ

     2. พื้นที่ใต้กราฟ M/EI ระหว่างจุดสองจุด คือ ค่าการเปลี่ยน slope ระหว่างสองจุดนั้น

วิธีการ

          

     1. เริ่มคำนวณโดยโดยแบ่งคานเป็นช่วงสั้น (dx)

     2. ที่จุด A ค่า deflection = 0 (yA = 0)  ค่า slope ที่จุด A เป็นค่าที่ยังไม่ทราบแน่นอน ให้ค่าเป็น 0 ไว้ก่อน (slope A = 0)

     3. คำนวณ slope จาก A ไป B โดยหาพื้นที่ใต้กราฟ M/EI  โดยเครื่องหมาย slope จะตรงข้ามกับเครื่องหมายของ M/EI   ,slopeB = slopeA+slopeAB

     4. คำนวณ ค่า y ที่ตำแหน่ง B  , yB = yA + slope*dx 

     5. ทำซ้ำในขั้นตอน 2 ถึง 4 ไปจนสุดปลายคาน

     6. ตอนนี้เราจะได้เส้นกราฟ deflection ที่มีความสัมพันธ์ระหว่างจุดถูกต้อง  แต่ตำแหน่งยังไม่ถูกต้อง

ต้องมีการคำนวณปรับแก้

     7. คำนวณปรับแก้เส้นกราฟ โดยยึดค่าที่จุด yA=0 และ yB=0  อาจใช้หลักการสามเหลี่ยมคล้าย

เริ่มคำนวณ      

พิจารณาคาน simple beam ยาว 6 ม. รับน้ำหนัก 10 kN/m  กำหนดให้ค่า E=200GPa ,I=16000cm^4

กรณีเราสามารถหาค่า deflection สูงสุดได้จากสูตร

ต่อไปเราจะลองใช้วิธีการแบบ numerical method เพื่อหาค่า deflection  ก่อนอื่นเราสร้างเส้นกราฟ BMD โดยใช้โปรแกรม MathCAD

ต่อไปเริ่มคำนวณ deflection curve ไล่ไปทีละจุด

ต่อไปลองนำค่าที่คำนวณได้มา Plot กราฟ

จะเห็นว่าเส้นกราฟยังไม่ถูกต้อง เพราที่จุดที่ x=6 ค่า deflection ต้องเป็นศูนย์  ในขั้นต่อไปเราจะคำนวณปรับแก้โดย ใช้เงื่อนไขดังกล่าว

ในที่นี้จะใช้การหมุนเส้นให้จุดปลายลงมาอยู่ที่ศูนย์  ก่อนอื่นหามุมที่ทำให้จุดปลายลงมอยู่ที่ศูนย์

เขียน rotation matrix

ลอง plot กราฟ จะเห็นว่าเส้นอยู่ในตำแหน่งที่ถูกต้องแล้ว

หาค่า deflection สูงสุด

จะเห็นว่าค่าใกล้เคียงกับค่าที่คำนวณจากสูตรสำเร็จ โดยมีความคลาดเคลื่อนประมาณ 4.4 % สามารถทำให้ค่าใกล้เคียงได้มากขึ้นโดยการเพิ่มจุดที่คำนวณให้ถี่ขึ้น

เราสามารถเขียนในรูปแบบ function ที่เรียกใช้งานได้ ดังต่อไปนี้

link สำหรับ MathCAD file >>>>https://drive.google.com/file/d/1X4vlFEe2TjwyioRMFaCK1oJadJwu9_Pk/view?usp=sharing

     ตัวอย่างสถานการณ์ที่สามารถนำความรู้จากบทความนี้ไปใช้ได้ คือ การคำนวณ deflection ของหน้าตัด prestress แบบ pre tension ซึ่งเมื่อรวมแรง prestress เข้าไปแล้ว กราฟจะมีลักษณะดังภาพต่อไปนี้

การคำนวณ - ด้านเสถียรภาพของกำแพงกันดินแบบ L

รูปแบบการวิบัติ

• Overturning : ป้องกันโดยคอนโทรลให้ตำแหน่ง Resultant Force อยู่ในระยะบวกลบ B/4 จากศูนย์กลางฐานรากกรณีฐานรากวางบนดิน หรือ บวกลบ 3B/8 สำหรับกรณีฐานรากวางบนหิน (หรือคอนโทรล F.S. ไม่น้อยกว่า 1.5 สำหรับการเช็คที่ service load โดยที่ F.S. = Mstabilize/Mdrive )

• Bearing Capacity : ป้องกันโดยไม่ให้หน่วยแรงอัดใต้ฐานเกินหน่วยแรงแบกทานที่ยอมให้ของดินใต้ฐาน การคิดหน่วยแรงกดใช้วิธี effective area (Be = B-2*e) ซึ่งจะได้เป็นหน่วยแรงแบบ Equivalent uniform pressure ใช้ในการตรวจสอบ Bearing capacity และการทรุดตัว เท่านั้น ( ส่วนการออกแบบตัวฐานรากให้คิดการกระจายแรงโดยการรวมหน่วยแรงปกติ คือ Stress = P/A + MC/I )

• Sliding : ป้องกันโดยไม่ให้แรงดันด้านข้างมีค่ามากกว่าแรงเสียดทานใต้ฐาน ใช้  Reduction Factor 0.80 สำหรับดินทราย 0.85สำหรับดินเหนียว (หรือให้ F.S. มีค่าไม่น้อยกว่า 1.5  สำหรับการเช็คที่ service load  โดยที่ F.S. = Fstabilize/Fdrive )

แรงที่มากระทำ

• dead load (DC) : คิดตามหน่วยน้ำหนักวัสดุ

• vertical earth pressure (EV) : คิดตามหน่วยน้ำหนักวัสดุ ประมาณ 1.8-2.0 ตัน/ตร.ม.

• lateral earth pressure (EH) : ในการเช็คเสถียรภาพให้ใช้ Active Earth Pressure Coefficient (ka)

• live load surcharge (LSV ,LSH) : น้ำหนักจรใช้ค่า 0.5-1.0 ตัน/ตร.ม. ขึ้นอยู่กับสภาพการใช้งาน

• wind load (if any) (W) : กรณีมีกำแพงให้คิดแรงลมด้วย คิดค่าแรงลมอย่างน้อย 50 กก./ตร.ม. หรือตามสภาพแวดล้อม

คิดแรงดันน้ำกระทำกับกำแพงไหม?

     โดย่สมมติฐานปกติจะไม่คิดแรงดันน้ำมากระทำต่อกำแพงกันดิน  จะใช้วิธีเตรียมรูระบายน้ำที่กำแพงเพื่อไม่ให้เกิดการสะสมของน้ำจึงไม่จำเป็นต้องคิดแรงดันน้ำ

เหตุผลที่ไม่ควรนำดินเหนียวมาเป็นวัสดุถมหลังกำแพง?

• การบดอัดดินเหนียวทำได้ยาก

• เมื่อการบดอัดที่สมบูรณ์ทำได้ยาก ก็ทำให้มีแนวโน้มจะเกิดโพรงปริมาณมากในเนื้อดิน ทำให้เกิดการทรุดตัวมากในภายหลัง

• ดินเหนียวบางชนิดมีการเปลี่ยนแปลงปริมาตรสูง เมื่อแห้งก็จะหดตัวจนเกิดรอยแตกกว้างที่ผิวดิน เมื่ออิ่มตัวด้วยน้ำก็จะพองตัว

สัดส่วนโดยประมาณของ ความสูงต่อความยาวฐาน ( ไม่รวมกรณีมีแรงลม )

ลองพิจารณเสถียรภาพต่อการ overturning

พิจารณาฝั่ง drive จะเห็นว่าแรงที่มีผลให้โครงสร้างล้มคว่ำคือ EH และ LSH

พิจารณาฝั่ง stabilize จะเห็นว่าแรงที่ต้านทานการพลิกคว่ำคือ EV

จากนิยามของอัตราส่วนความปลอดภัย 

แทนค่าสมการจะได้

ใช้ MathCAD ช่วยลดรูปสมการฝั่งซ้าย จะได้

จัดสมการใหม่ ให้อยู่ในรูป function ของ Hw

สมมติค่าพารามิเตอร์ต่างๆ ดังนี้

กำหนดค่าตัวแปร

ใช้โปรแกรม MathCAD ช่วยหาคำตอบ

ลองหาอัตราส่วนระหว่างความกว้างฐานต่อความสูง

จะเห็นว่าที่ความสูง 1 ม. ต้องการความกว้างฐาน 55% ของความสูง  อัตราส่วนจะค่อยๆลดลงตามความสูง  จนที่ความสูง 8 เมตร จะต้องการความกว้างฐาน 42.8% ของความสูง

ถ้า plot กราฟความสัมพันธ์ระหว่าง ความสูงในแกนตั้ง กับความกว้างฐานในแกนนอน จะได้ดังนี้

ต่อไปลองพิจารณเสถียรภาพต่อการเคลื่อนตัวด้านข้าง

พิจารณาฝั่ง drive จะเห็นว่าแรงที่มีผลให้โครงสร้างเคลื่อนตัวคือ EH และ LSH

พิจารณาฝั่ง stabilize จะเห็นว่าแรงที่ต้านทานการเคลื่อนที่คือ EHP และ f

จากนิยามของอัตราส่วนความปลอดภัย 

แทนค่าสมการจะได้

ใช้ MathCAD ช่วยลดรูปสมการฝั่งซ้าย จะได้

จัดสมการใหม่ ให้อยู่ในรูป function ของ Hw

สมมติค่าพารามิเตอร์ต่างๆ ดังนี้

ใช้โปรแกรม MathCAD ช่วยหาคำตอบ

ลองหาอัตราส่วนระหว่างความกว้างฐานต่อความสูง

จะเห็นว่าที่ความสูง 1 ม. และ 2 ม. ผลลัพธ์มีค่าติดลบแสดงว่าแรงผลักทั้งหมดไม่ชนะแรง Passive ที่ต้านทานอยู่  ที่ระดับ 2 ม. จะเริ่มต้องการแรงเสียดทานมาช่วย โดยความกว้างที่ต้องการมีค่า 12.7% ของความสูง  และค่าจะเพิ่มขึ้นเรื่อยๆ จนที่ความสูง 8 เมตร จะต้องการ ความกว้างฐาน 48.9% ของความสูง

ถ้า plot กราฟความสัมพันธ์ระหว่าง ความสูงในแกนตั้ง กับความกว้างฐานในแกนนอน โดยPlot ลงในกราฟเดียวกับ กรณี Overturning จะได้ดังนี้

จากกราฟด้านบน จะเห็นว่าเกิดจุดตัดกราฟที่ความสูง ประมาณ 6.435 ม.  ความสูงที่ต่ำกว่าความสูงนี้พฤติกรรม overturning จะเป็นตัว control ความต้องการความกว้างของฐาน  ส่วนความสูงที่มากกว่า 6.435 ม. พฤติกรรม sliding จะเป็นตัว control

ผลลัพธ์ดังกล่าวนี้เป็นจริงเฉพาะค่าพารามิเตอร์ที่ใช้ในการคำนวณ ณ ที่นี้เท่านั้น  ไม่สามารถใช้อ้างอิงได้ในกรณอื่นๆซึ่งต้องพิจารณาจากคุณสมบัติของดินเป็นสำคัญ  แต่อย่างน้อยก็ทำให้เรารู้แนวโน้มว่าผลลัพธ์จะประมาณเท่าไร

link ไฟล์ MathCAD >>>  https://drive.google.com/file/d/1aWzrdcRO_z-i6LMRt_AVuOLPd7BGnlZF/view?usp=sharing